Първа публикация: 06-02-2013

Последна редакция: 10-06-2015

Реминисценция +

Преди десетина дни бе публикувана кратката, но показателна студия "Магия и числа / или Числа и магия". От споделените отзиви можеше да се заключи, че нейното съдържание е подложило на изпитание здравия разум на мнозина.

Всъщност, Зенон и неговите апории далеч не са единствените предизвикателства пред човека, в това число и пред онзи, който владее тънкостите на прецизното математическо мислене. През вековете хората са натрупали огромен резерв от подобни задачи и – доколкото те много често изискват върхово интелектуално напрежение – при успешен изход чувството за удовлетворение е огромно. (И е заразително! Поражда желание за следващо изпитание.)

И така...

ДАДЕНО:

Един син поискал от родителите си пари назаем – бил харесал някаква риза и пожелал да си я купи. Ризата струвала 97 лева. Синът получил от майка си и от баща си по 50 лева. Купил си ризата, при което му били върнати 3 лева.

Прибирайки се вкъщи, той възстановил по един лев на майка си и на баща си. По такъв начин дългът към родителите му намалял с по един лев. Третия лев от рестото задържал у себе си.

Внезапно обаче синът съобразил, че се е случило нещо много странно. Сумата от намалените дългове към родителите му възлизала на 98 лв. (49 лв. + 49 лв. = 98 лв.). Щом към нея се прибавел левът, който той задържал у себе си, се получавал резултат от 99 лв.

ПИТА СЕ:

Къде се губел 1 (един) лев?

РЕШЕНИЕ:

Нека сега бъде разгледана идентична задача, при която са променени само някои от числовите данни – цената на ризата и частите от рестото, възстановени на родителите:

При този резултат следва да сме изненадани от увеличилата се сума на "губещи се" левове. Това може да ни подтикне да направим и следваща стъпка – с едно по-чувствително намаление при цената на ризата и, съответно, по-чувствително завишаване на възстановената част от дълга към родителите:

Разбира се, можем да продължим с изследването на динамиката около крайния резултат. Можем, например, да проявим интерес към онова, което би се случило, ако ризата би била с цена 1 лв. (да речем, оказала се е закупена като преоценена стока):

Със сигурност, при такъв последен резултат и у най-несведущия в областта на елементарните аритметични операции би се появило усещането за някаква системна грешка, неволно допусната (или майсторски скрита) още в предложения модел за разсъждение.

Къде може да се крие тя?

Вероятно няма да се намери по света учител по математика, който да не е предупреждавал многократно своите ученици, че – образно казано – не могат да събират "круши" с "ябълки". И по-точно: че те не могат да правят това, докато в една задача "крушите" остават круши, а "ябълките" – ябълки. Ако обаче попътно въпросните артикули бъдат обявени за "плодове", тогава с тях (и между тях) могат да бъдат извършвани всякакви операции.

В горната схема на разсъждения, в т. 11 се събира "дълг" с "наличност". Разбира се, в случай на необходимост и тук може да се осъществи понятийна трансформация, при която, примерно, съответните стойности за дълг и наличност да се мислят като "пера от счетоводен баланс" с противоположни знаци ("+" и "–") – всичко това, да речем, с цел уточняване на окончателното състояние на баланса, който във всеки идеален случай би трябвало да възлиза на: 0,00 лв. Ето един примерен вариант на такъв отчет, интерпретиран през погледа на сина:

Както се вижда, в него няма (а и не може да има) никакви "губещи се" суми.

Условието на задачата може да бъде интерпретирано и в по-олекотен вариант. Например, би могло да се приеме, че с възстановяването на част от дълга към родителите (по 1 лв. към всеки от тях) синът фактически е получил заем от 98 лв. (по 49 лв. от всеки от тях). В такъв случай отчетът би изглеждал така:

Отново се вижда, че няма никакви "губещи се" суми.

Безусловно, от най-стари времена математиката и математиците респектират целия останал свят. Понякога той им отвръща с подобаващо унищожителни средства – сякаш за да покаже, че и придворните, които обслужват царицата на науките, далеч не са толкова безупречни в своето пословично мисловно съвършенство, колкото мълвата ги представя. Едно от най-злостно преследваните отмъщения се домогва до следната, по плебейски семпла, цел: да се внуши, че с математически средства може да бъде доказано всичко, което някой предварително си е наумил! (Дори и то да представлява връх на абсурда!)

Ето пример.

ДАДЕНО:

Никой не би възразил срещу написването на уравнение от рода на долното: a = b. То би отразило една често срещаща се ситуация в живота – равенството на две величини.

Разбира се, след като такова равенство е положено като изходно условие, то всяко мислимо произведение на първата величина със самата себе си, може да бъде представено като произведение и между двете различни като обозначение, но еднакви като стойност, величини. Така, резултатът не би се променил, ако в умножението на а с а едното а бъде заменено с равнозначното му b.

Последващата трансформация на уравнението (вариант № 3) е не по-малко закономерна: ако от две равни стойности се извади една и съща величина, двата получени резултата са също равни. В конкретния случай еднаквият умалител е квадратът на b.

Във варианта под № 4 уравнението е претърпяло математическа процедура, известна като разлагане на многочлени: в лявата страна – чрез предварително доказана формула, а в дясната – чрез изваждане на общ множител (b) пред скоби. Тук, за да не се остане с впечатлението за нещо , което се скрива от публиката, нека бъде направена следната проверка:

(a + b) (a – b) = a² – ab + ab – b² = a² – b².

След това преобразуване, в двете страни на уравнението се появява един и същ елемент, множителят: (а – b).

Известно е, че всяка страна на едно равенство може да бъде разделена на едно и също число, без подобна манипулация да промени характера на равенството. В достигнатата трансформация на уравнението, това е споменатият множител (а – b). След като двустранното разделяне се извърши, се стига до вариант № 5.

Тук отново може да бъде припомнено изначалното полагане (а = b), след което а да бъде заменено с b. В резултат се получава вариант № 6 на равенството, който вече известява достатъчно красноречиво достигнатия абсурд: 2b = b.

С последното видоизменение (чрез двустранно разделяне на уравнението с b) се достига до квинтесенцията на заниманието: 2 = 1.

ПИТА СЕ:

Има ли грешка в осъществените математически трансформации? Ако отговорът е: "Да", къде е тя?

РЕШЕНИЕ:

Грешката се съдържа в трансформацията от вариант № 4 към вариант № 5 на разглежданото уравнение. На пръв поглед, там няма нищо нередно: двете страни на уравнението са разделени с едно и също число – в случая, представено чрез делителя (а – b).

Ако обаче не е забравено началното полагане, а именно: а = b, ако заедно с това се направи опит да се пресметне числовото изражение на израза (а – b), веднага ще бъде забелязано, че то възлиза на 0 (нула):

a – b = a – a = 0.

В такъв случай се оказва, че в прехода от вариант № 4 към вариант № 5 на въпросното уравнение е извършена забранена в аритметиката процедура: деление с нула!

Обичайно, в математиката делението се определя като процедура, обратна на умножението. Доколкото всяко произволно число (примерно, n), умножено по нула (примерно, обозначена като z – "zero"), води до резултат 0 (нула),

n . z = 0,

то не би следвало да съществува число, различно от 0, което да се явява резултат от умножение по 0. В такъв случай, обратният процес: 0, разделена на 0, би трябвало да води до всяко произволно число (n) – нещо напълно неопределено, за да може да бъде мислено като резултат.

След като делението се определя чрез умножението, може да възникне въпросът: как се определя самото умножение? Една възможност се открива в следната идея: умножението представлява частен случай на операцията събиране, при която събираемите са равни едно спрямо друго.

На свой ред, събирането се интерпретира като основополагаща операция, при която се осъществява съпоставяне на елементите, принадлежащи на две крайни множества, с елементите на трето (също крайно) множество по такъв начин, щото всеки от елементите на първоначално зададените множества да е елемент и на третото множество.

Независимо от забраната за извършване на деление с нула, в математиката се счита, че изрази от рода на n / 0 могат да бъдат свеждани по смисъл до представата за безкрайност, при условие че не се правят опити те да бъдат третирани според обичайните правила за смятане с числа.

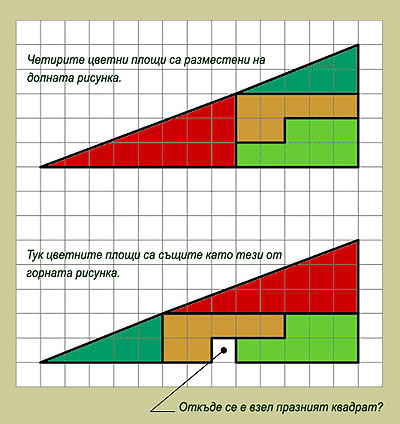
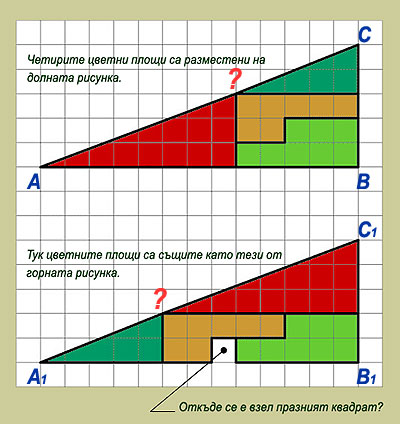
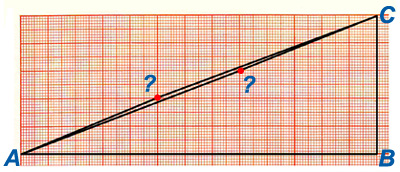
ДАДЕНО:

Условието на настоящия геометричен парадокс е видно от двата чертежа вляво.

Правоъгълен триъгълник е разделен на четири планиметрични фигури: два правоъгълни триъгълника и два вдлъбнати шестоъгълника (за удобство, всички фигури са представени в различни цветове). Както се вижда, площите и на четирите фигури се вписват изцяло в големия правоъгълен триъгълник.

Ако сега мислено си представим, че съставните фигури са изработени от отделни цветни картони, бихме могли да ги разместим по начина, по който това е сторено на долния чертеж. Изненадващо, едно квадратче остава незаето.

ПИТА СЕ:

Къде се крие причината за появата на празната площ?

РЕШЕНИЕ:

За решението на възбудения проблем може да се подходи по два начина: при първия би следвало да се разчита на остротата на зрението или на точността при извършване на определен кръг чертожни манипулации, докато при втория резултатът би се получил от стриктни логически стъпки, съпътствани от не по-малко стриктни изчислителни процедури.

Ако се погледне с необходимата съсредоточеност върху дословното повторение на горната графика и ако фокусът на вниманието бъде насочен към местата, обозначени с червени въпросителни (на свой ред те могат да се третират като буквени символи на геометрични точки), то може да се забележи, че "отсечките" АС и А1С1 далеч не представляват отсечки. В този смисъл, те не са части от прави линии, а съчетания от по две отсечки: в горния "триъгълник" (АВС) това са отсечките А? и ?С, а в долния "триъгълник" (А1В1С1) – отсечките А1? и ?С1. По същата причина, така наречените "триъгълници", АВС и А1В1С1, са всъщност четириъгълници, като този от фигурата АВС? е вдлъбнат (ъгълът при точка ?, погледнат откъм вътрешността на многоъгълника, е по-голям от 180°), а онзи от фигурата А1В1С1? е изпъкнал (идентичният ъгъл при точка ?, погледнат откъм вътрешността на многоъгълника, е по-малък от 180°).

От изложеното дотук следва, че площта на фактическия четириъгълник АВС? е по-малка от тази на предполагаемия "триъгълник" АВС (АВ . ВС / 2 = 13 . 5 / 2 = 32,5 квадратни единици), докато площта на фактическия четириъгълник А1В1С1? е по-голяма от идентичната площ на предполагаемия "триъгълник" А1В1С1. От тези разлики се формира площта на "появилото се от нищото" празно квадратче.

Ако двете фигури, АВС и А1В1С1, разглеждани погрешно като правоъгълни триъгълници, бъдат наложени една върху друга (така, както това е сторено на чертежа върху милиметровата хартия), ще бъде забелязано, че те не се покриват и че фактически имат различни площи. Площта на тънката ивица, заключена между двете точки, отбелязани с въпросителни, и точките А и С – площ, която по същество представлява силно сплескан ромбоид – дава обяснението за произхода на празното квадратче.

Едно друго обяснение на причината за възникване на парадокса може да бъде установено със следните разсъждения.

Ако двете фигури от горните цветни изображения, АВС и А1В1С1, бяха действително правоъгълни триъгълници (сиреч, ако точките, отбелязани с въпросителни, лежаха върху действителни отсечки: АС, респективно А1С1), то тогава двата вградени правоъгълни триъгълника, оцветени в червено и тъмнозелено, би следвало да са подобни един на друг. Едно от свойствата на подобните триъгълници се свежда до равенство на съответните им ъгли. В случая, това би означавало следното: долният ляв ъгъл на червения триъгълник да е равен на долния ляв ъгъл на тъмнозеления. (Между другото, същият извод би последвал и от теоремата за пресичането на права линия с две успоредни прави линии, каквито в настоящия пример са черните хоризонтални линии от все същите цветни фигури. Естествено, това би се случило единствено, ако двойките отсечки А? и ?С, респективно А1? и ?С1, лежаха върху прави линии.)

При положение, че коментираните ъгли на въпросните съставни триъгълници бяха равни, то от това би последвало, че, примерно, тангенсите на тези ъгли (измерващи се със съотношението на срещуположния към прилежащия катет) също би трябвало да бъдат равни. В конкретния случай тангенсите могат да бъдат изчислени. Това би означавало да се пресметне съотношението между числата 2 и 5 (за тъмнозеления триъгълник) и 3 и 8 (за червения триъгълник). Както веднага може да се установи, първото число би било: 2 / 5 = 0,4, докато второто би било: 3 / 8 = 0,375. Оттук, тангенсът на долния ляв остър ъгъл на тъмнозеления правоъгълен триъгълник би бил: 0,422793 (а това би съответствало на ъгъл от около 23°), докато тангенсът на идентичния долен ляв остър ъгъл на червения правоъгълен триъгълник би бил: 0,393627 (нещо, което би съответствало на ъгъл от около 21,5°. С това отново се доказва, че хипотенузите на двата съставни правоъгълни триъгълника не лежат (и не могат да лежат!) върху "хипотенузата" на някакъв "правоъгълен триъгълник" АВС (или А1В1С1), доколкото такъв триъгълник изобщо не съществува.

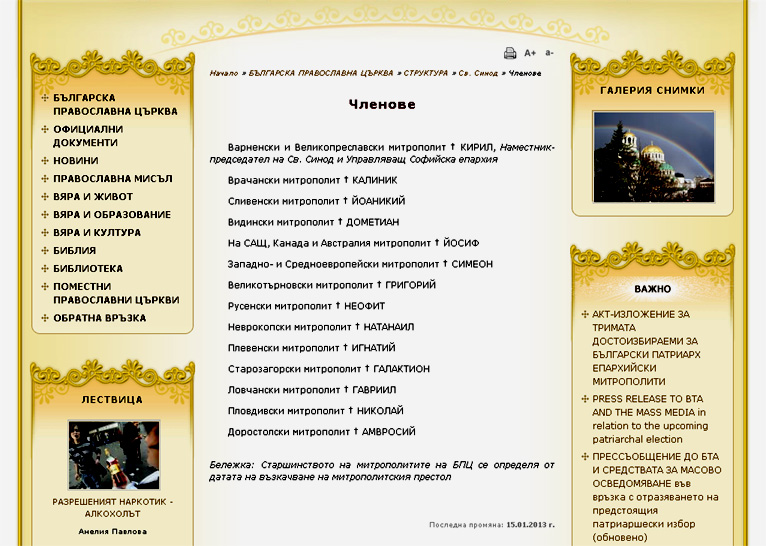
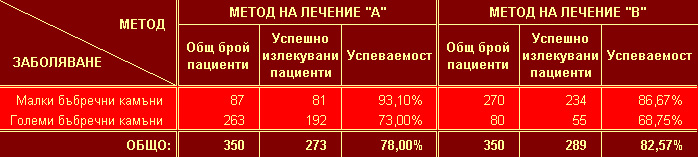
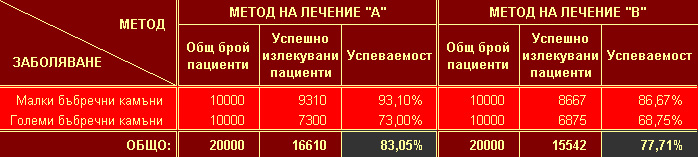
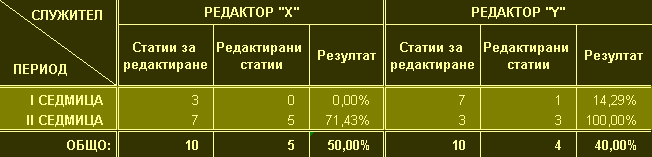
2. Съставът на Светия Синод на Българската православна църква е:

3. Съдържанието на специалния синодален акт, с който от Светия Синод на Българската православна църква се обявява изборът на "трима епархийски митрополити", в качеството им на "достойни кандидати" за "Патриаршеския престол", гласи:

ПИТА СЕ:

Коректен ли е изборът на тримата кандидат-патриарси?

РЕШЕНИЕ:

Преди да бъде предложено решение на поставения въпрос следва да бъде анализиран внимателно текстът на чл. 45 (1) от Устава на Българската православна църква. По-специално, това се отнася до повелението за

необходимо при избора на

“трима кандидати за патриаршеския престол”.

От чисто математическа (и стриктно логическа) гледна точка, предписаното изискване може да се спази само в някои частни случаи. Например: ако Светият Синод е съставен от 12 души и със "за" са гласували 8 души или ако съставът му е от 15 души и гласовете "за" са 10. И така нататък. (Сиреч, във всеки случай, при който съставът на въпросния орган се представя с число, кратно на 3: 3, 6, 9, 12, 15 и прочее, а сумата от гласове "за" се представя със съответно число, кратно на 2: 2, 4, 6, 8, 10 и прочее.)

Все в този дух на разсъждение, при състав от 14 души, никога не би могло да се постигне уставно записаното мнозинство, доколкото 2/3 от 14 не е цяло число. (Тук може да се стори излишно да се обяснява, че изискването за резултат "цяло число" не е някаква самоцел, а е продиктувано от факта, че нито отделният член на Синода може да бъде разделян на части, нито това може да бъде направено с неговото заявено становище ("за" или "против"). И архиереите, и техните записани върху бюлетините мнения, са неделими цели единици.)

Съвършено друго би било положението, ако текстът от въпросния уставен член гласеше: мнозинство, не по-малко от две трети от членовете. За съжаление, такъв текст липсва.

Ако обаче временно бъде допуснато, че изразът “мнозинство от две трети от членовете на Светия Синод” следва да се мисли като: “мнозинство, НЕ ПО-МАЛКО ОТ ДВЕ ТРЕТИ от членовете”, то тогава трябва да се приложи елементарната аритметична операция за изчисляване на част от цяло. В такъв случай е необходимо да се извърши последователно деление на:

1. числото 10 на числото 14 и

2. числото 9 на числото 14.

Резултатите са съответно:

1. 0,714286 и

2. 0,642857.

Първият резултат представлява число, по-голямо от 2/3 (или 0,66666(6)), а вторият – по-малко от 2/3. Следователно, единствено изборът на старозагорския митрополит Галактион в качеството му на кандидат за "патриаршеския престол" е процедурно коректен, а така нареченият "избор" на другите двама митрополити е фактически недействителен. Съпътстващо, невярно е и внушението от текста на рекапитулиращия синодален документ ("Акт-изложение"), в който се казва:

доколкото нито 2/3 от 14 е 9, нито останалите двама кандидати са действително "избрани".

В обширния си трактат "Беседи и математически доказателства относно две нови науки" Галилео Галилей, представяйки едни или други свои научни идеи под формата на диалози между трима участници, пише:

“Салвиати (към събеседниците си Сагредо и Симпличо): Вие отлично знаете, предполагам, кои числа могат да бъдат квадрати и кои не?

ПИТА СЕ:

“Сагредо: И какво трябва да решим в случая?”

РЕШЕНИЕ:

Преди да се пристъпи към разглеждане на възбудения казус изглежда подходящо да се посочи, че въпросният парадокс само условно е наречен "Парадокс на квадратите". С не по-малко основание (и след някои несъществени промени в параметрите на заданието) той би могъл да се превърне, примерно, в "Парадокс на кубовете" (или, казано с други думи, на "третите степени"). Продължавайки в същата посока, парадоксът би могъл да стане Парадокс на четвъртите, петите, шестите и така нататък степени. Най-общо, той би могъл да получи титула "Парадокс на N-тите степени". По такъв начин лесно би се забелязало, че всяка интерпретация на "Парадокса на квадратите" може да се третира като интерпретация и на всяка друга версия на все същия логически проблем, независимо от използваното степенно число. Нещо повече, би се забелязало, че колкото степенният показател е по-голям, толкова по-големи са пространствата, запълнени с естествени числа, които не могат да се разглеждат като резултат от повдигане на степен, и толкова по-стръмно тези пространства нарастват вътре в собствените си числови редици (тези на вторите, третите четвъртите и така нататък степени).

За да се провери това твърдение, може да се разгледа долният фрагмент от числова таблица, който съдържа първите 32 позиции от редицата на естествените числа (които на свой ред спокойно могат да бъдат мислени и като резултати от повдигане на първа степен). След това може да се направи сравнение с разположените над тях редици от същите числа, сред които са откроени в червен цвят резултатите от поетапните повдигания на числата 1, 2, 3 и така нататък на втора, трета и четвърта степен:

Таблица 1

Безусловно, в такава ситуация изглежда разумно най-напред да бъде припомнена дефиницията на понятието "естествено число" ("естествени числа"). За съжаление, дори и днес това може да се окаже проблематично, доколкото битуват различаващи се мнения.

Така например, българските ученици учат (и трябва да запомнят), че числото 0 (нула) "не е естествено число". От друга страна, в математическата справочна литература може да се срещне изричното твърдение, че то "е естествено число". (Вж. във връзка с това: Валтер Гелерт, Херберт Кестнер и Зигфрид Нойбер, "Математически енциклопедичен речник", София, 1983, с. 381.)

Наистина, когато Джузепе Пеано обявява своите аксиоми, имащи отношение към свойствата на естествените числа, той включва в първото си твърдение редицата от числа, която започва с числото 1: 1, 2, 3 и така нататък. По-късно обаче, когато нулата получила статута на така наречената "добавена идентичност", тя била включена към естествените числа. Именно по този начин, за всички елементи от тази редица числа, се оказало възможно да имат по един предшественик и по един наследник, отстоящи на единица, като само за нулата се оказало изпълнимо условието да

Нека сега си представим, че горната серия от 32 числа се е увеличила с още едно – нулата, и нека, заедно с това, съсредоточим мислите си само върху въпроса за квадратите:

Таблица 2

Нека направим и една първа следваща крачка и си представим, че коментираната редица от естествени числа е съставена от краен брой елементи (колкото и това да е в контраст със самото дефиниционно изискване всеки неин елемент да се получава от предходния с добавянето на единица). Нека първоначално този брой да е 5 и да обхваща числата от 0 до 4 включително:

Таблица 3

Както се вижда, две от първите пет естествени числа (3 и 4) не могат да изиграят ролята на "страни" (или "корени"), защото техните "квадрати" (9 и 16) излизат извън дефинирания обсег (0 – 4). Освен това, две от числата, представляващи "квадратите", 2 и 3, нямат свои "страни" ("корени"), защото никое от числата между 0 и 4 не може да произведе от умножение със самото себе си "квадрат" с въпросните стойности (2 и 3). При това положение "коефициентът на полезно действие" (КПД) – ако подобен израз е подходящ в случая – който може да се припише на страните (корените) по отношение на произвежданите от тях квадрати, разбираемо, е 3/5 (или 0,60).

Ако сега си представим, че редицата от естествени числа е разширена, че вече е съставена от по-голям краен брой елементи и този брой е 10: от 0 до 9 включително, то идентичната таблица би изглеждала така:

Таблица 4

В случая, предложеният КПД би бил 4/10 (0,40). Това говори еднозначно, че в настоящия числов отрязък (от 0 до 9) възможностите за произвеждане на квадрати са по-малки, отколкото в предходните по-тесни граници. Много повече числа (6) нито могат да произведат квадрати, нито могат да бъдат третирани като нечии квадрати.

Ако предприетото постепенно увеличаване на числовата област бъде продължено (при запазване на изначалното условие тя да бъде изпълнена с краен брой числа), то картината би била следната:

Таблица 5

Коментираният КПД тук би бил 5/17 (или приблизително 0,29).

Следващата стъпка би изглеждала така:

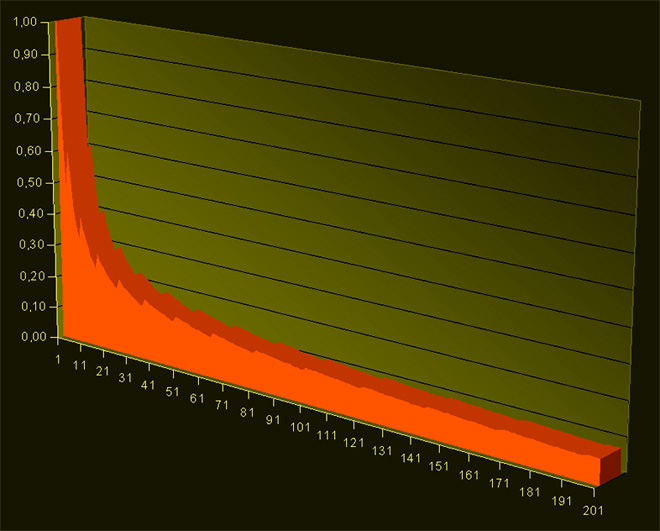
Таблица 6

КПД би бил 6/26 (или приблизително 0,23).

Ако се продължи по същия начин, неминуемо ще се забележи закономерност, която – дори и само интуитивно – следва вече да е доловена: колкото повече се увеличава обхватът на числовата област, в която се изследва бройката връзки: страни (корени) – квадрати, толкова повече те намаляват спрямо общия брой числа, формиращи съответната област. Илюстративно, тази закономерност се вижда на долната графика, която отразява картината при първите 201 естествени числа (от 0 до 200 включително):

Вероятно у никого не би могло да се появи съмнение, че с увеличаването на броя естествени числа, формиращи областта, в която се изследват количеството споменати връзки (страни (корени) – квадрати), делът на все същите връзки намалява. При това, колкото и този дял да става все по-малък и по-малък на фона на все по-големите бройки естествени числа, той никога не би могъл да стане нула. Във всеки конкретен случай обаче, при който се разглежда каквото и да било конкретно количество поредни естествени числа, ще има числа, които ще бъдат част от съответствието страна (корен) – квадрат, и такива, които или ще бъдат страни (корени) без свои квадрати, или "претенденти" за квадрати, които нямат свои страни (корени).

И което е най-важно – няма да има никакъв парадокс! А колкото и това да се стори излишно, нека попътно бъде подчертано още веднъж: няма и никакви безкрайни съвкупности от елементи, към които да се правят опити да се прилагат понятия и процедури, използвани при крайните съвкупности.

Нека сега отново бъде разгледан един фрагмент от текста на Галилео Галилей – и по-специално, следната реплика на Салвиати:

“Така че, ако аз кажа, че всички числа, включващи както квадратите, така и не-квадратите, са повече от квадратите, това ще бъде съвсем вярно твърдение.”

Ако към тази мисъл се подходи с разбирането, което бе засвидетелствано дотук, в нея не би могло да се открие нищо нелогично. Всъщност, тя е повторение на онова, което се вижда на таблици №№ 2-6: при тях въпросните "всички числа" са включени в долните редове, а квадратите (оцветени в червено) – в горните. Дори и да се дистанцираме от тази конкретика, никой не би се усъмнил в твърдения, които представляват частни проявления на принципа: частта е винаги по-малка от цялото.

Нека обаче сега се вгледаме внимателно в някак неусетно промъкналия се израз "всички числа". Първият въпрос, който би следвало да си зададем, може да бъде формулиран така: имаме ли право да употребяваме този израз, след като от контекста се разбира, че става (или ще става) въпрос за всички числа изобщо. Още повече, че в последната цитирана мисъл Салвиати говори именно за "всички числа изобщо". Не за всички числа от едно крайно множество, а за всички числа от някакво мислимо безкрайно множество. При това, не в качеството им на философска представа, а като обект, с чийто брой ще трябва да бъдат извършвани някакви съпоставяния и/или елементарни аритметични действия (примерно, изчисления на част от цяло).

При такива обстоятелства, зададеният непосредствено по-горе въпрос може да бъде последван от друг: знаем ли – и имаме ли възможност да знаем – броя на всички числа? Лесно може да се допусне, че всеки ще отговори с "Не". Тогава идва редът на по-нататъшното питане: ако не знаем броя на всички числа, то имаме ли право да мислим за едни или други сравнителни и/или изчислителни процедури, в които явно или неявно този "брой" се включва? Възможно ли е представата за каквато и да било безкрайна редица от елементи (а естествените числа са именно такава редица от елементи) да се свързва с някакво конкретно число? И тук наложителният – и единствено правилният – отговор е "Не". Изрази като: "N е равно на безкрайност" или "броят на естествените числа е равен на безкрайност", са лишени от какъвто и да било смисъл. Безкрайността може да бъде мислена само като някакъв процес, за който се предполага, че може да се разгръща неограничено, без това предположение да се приема като доказателство за възможността той да бъде непременно материално осъществим.

В случая може да се предполага (но именно: само да се предполага!), че Галилей е включил по подвеждащо невинен начин израза "всички числа", защото приведеният в условието на задачата диалог продължава по следния начин:

“Салвиати: И в последна сметка ще трябва да се съгласим, че свойствата ‘равен’, ‘по-голям’ и ‘по-малък’ не са приложими по отношение на безкрайните, а само по отношение на крайните величини.”

Попътно пояснение. В цитирания в началото диалог се съдържа и една принципна неточност. В един момент Салвиати твърди, че

“всеки квадрат има свой корен”.

Говорейки в единствено число, той добавя, че

“нито един квадрат не може да има повече от един корен”.

Това не е вярно. Днес се знае, че "всеки квадрат" има два корена: един положителен и един отрицателен. Доколкото обаче самото въвеждане на отрицателните числа в корпуса на математиката е представлявало бавен и мъчителен процес, проточил се дълго след смъртта на Галилей, той следва да бъде извинен за застъпеното становище.

Съществува народна поговорка, която казва:

ПИТА СЕ:

Съдържа ли се в поговорката логическо противоречие?

РЕШЕНИЕ:

Дефинираният въпрос провокира необходимостта от някои предварителни уточнения.

Например, може да се изкаже предположението, че текстът на цитираната поговорка има за цел да предпази човека от извършване на най-голямото – реално или мислимо – зло: спора, несъгласието, борбата (или, както е казано в случая, "караницата") с "Бога". Ето защо, пред подобна перспектива – съветва поговорката – е по-добре да се извърши което и да било друго зло ("изговарянето на голяма дума" – символ на горделивостта), отколкото да се влиза в конфликт с "Твореца на всичко видимо и невидимо". От такава позиция може да се приеме, че поговорката не носи никакво логическо противоречие, доколкото е в синхрон с известната друга народна мъдрост:

Може да се разсъждава и по друг начин. Посланието на поговорката да се интерпретира като насочено и отнасящо се само до религиозните хора – тези, които живеят със съзнанието, че имат точна представа за обекта на своите мисли, обозначаван с думите "Бог" или "богове". За всички останали би могло да се твърди, че втората половина на поговорката, а оттам и цялата поговорка, следва да е лишена от какъвто и да било смисъл. В резултат, такава категория хора не би могла да отстоява тезата, че сентенцията носи противоречие, доколкото всяко противоречие може да бъде търсено (и евентуално намирано) единствено там, където всички елементи на изследваното твърдение носят някакъв смисъл.

От друга страна, може да се обърне внимание върху факта, че дори и тогава, когато нерелигиозни хора участват в разговори за "Бог" или "богове", те правят това в контекста на някакъв кръг религиозни определения и представи за въпросните върховни инстанции. Образно казано, те – нерелигиозните хора – влизат частично в коловоза на религиозното мислене. В противен случай никакъв разговор не би бил смислен и изобщо – възможен. Оттук би следвало да се направи противоположният извод: че поговорката има много по-голяма фактическа насоченост. И дори тя да не може да се измерва с теоретичната общност на всички хора по земята, в чисто практически аспект може да се приеме, че има точно такъв статус.

Сега вече може да се погледне към съдържанието на предложената сентенция.

"Карането" (употребено в смисъл на "участие в скандална препирня") се осъществява в речева форма. От това следва, че и в първата, и във втората половина на поговорката става въпрос за речеви действия – валидни дори и за немите хора, доколкото те също разговарят (в това число – и се карат), независимо че не огласяват нито една дума. Тук лесно може да се приеме за достатъчно истинно твърдението, че техните жестикулации, придружени от съответни мимически изражения, представляват вид говор, напълно съпоставим с традиционно разпространеното звуково словесно общуване.

След като и в първата, и във втората половина на поговорката става въпрос за речева активност, се налага да се уточни понятийното съдържание на израза "голяма дума". Недвусмислено, той се употребява тогава, когато се изказва някаква обективно важна мисъл или се демонстрира претенция, че огласяваното твърдение е от извънредна важност. Както бе посочено, за хората, които говорят "големи думи", в общественото съзнание е закрепена традиционна негативна представа като горделиви, високомерни, голеемеещи се. От друга страна, всеки, който би дръзнал "да се кара" с "Бога", би следвало да разглежда себе си като равностоен "Нему", което означава, че такъв човек трябва дефинитивно да обладава именно изредените качества и като така да говори несъмнено "големи думи", когато "се кара" с "Бог".

В такъв случай, всяко действие от първата половина на поговорката трябва да се мисли като акт на надменност, осъществяван без значение на формата, в която се изразява, както и на адресата, към който се насочва. В допълнение, всяко действие от втората половина на все същата поговорка трябва да се мисли като частна проява на надменност, осъществявана: 1. в конкретна ("гневна") форма, и 2. по отношение на отделен конкретен адресат. Лаконично изречено, всяко поведение, описано в тази втора половина на сентенцията, се явява: 1. подмножество на надменното поведение изобщо, и 2. подмножество на подмножеството на въпросното надменно поведение (надменното поведение от първата половина на поговорката).

Отправяйки разсъжденията в руслото на "Теория на множествата", следва да се припомни фундаменталното положение, по силата на което всички характеристики на елементите, принадлежащи към някакво множество, са характеристики и на елементите от съответното подмножество, но не всички характеристики на елементите, принадлежащи към определено подмножество, са характеристики и на елементите от изходното множество (понякога наричано по аналогия "надмножество").

В случая, говоренето на “големи думи” (изобщо) може да се разгледа като някакъв изначален тип словесно поведение, чиито прояви представляват елементи на изходното множество (в горната графика те изпълват пространството на най-големия кръг). Негово подмножество се явява говоренето на “големи думи” с гняв (ако се приеме така да се обозначава всяка проява на "кавга", "караница", "свада", "разпра", "раздор", "крамола", "скандал" и прочее). Разбираемо, характеристиката "с гняв" се явява отличителен белег на проявите от въпросното подмножество (които, също толкова разбираемо, изпълват пространството на средния кръг). Накрая, подмножество на предходното подмножество се явява говоренето на “големи думи” с гняв към “Бог” (което, след направените допускания, представлява синоним на фразата: "с бога да се караш"). Лесно се разбира, че добавката "към 'Бог'" превръща проявите от това последно подмножество в частни случаи на говоренето на “големи думи” с гняв (изобщо).

Ако сега се направи необходимата рекапитулация, ще се установи, че:

1. Не е възможно да се осъществява "караница" с "Бог" без да се изговарят "големи думи".

2. Не е възможно да се дава съвет, по силата на който е по-добре да се изговори "голяма дума", нежели да се прави "караница" с "Бог", след като това би означавало да се огласява препоръка, еквивалентна на следната безсмислица:

Освен всичко изложено дотук, изглежда разумно проблемът да бъде разгледан и от една друга гледна точка. Нека бъде поставен следният въпрос: възможно ли е някой да изговори "голяма дума", с което да изпълни предписаното поведение ("по-добре голяма дума да продумаш"), и в същото време в тази голяма дума да няма дори и намек за "караница" с какъвто и да било "Бог" или "богове"? Една първа реакция подсказва, че това изглежда възможно. Например, по всичко личи, че народната поговорка-закана:

може да бъде считана за елемент от множеството "Говорене на 'големи думи'", като в същото време е елемент и на подмножеството "Говорене на 'големи думи' с гняв ('караница')". Заедно с това, всичко подсказва, че тя не може да бъде разглеждана като елемент от под-под-множеството "Говорене на 'големи думи' с гняв ('караница') към 'Бог'".

Ненадейно обаче, тук се отваря много голям смислов проблем – изниква следващият въпрос: какво трябва да се разбира под "караница"? Има хора, които приемат и най-деликатно изказаното несъгласие като кавга, раздор и прочее. Еталонен образец в това отношение е следният английски виц:

Ако сега се запитаме: има ли "големи думи" в известната поговорка:

вероятно ще трябва да отговорим с "Да". Има "големи думи", защото се внушава непоколебимата увереност в това, че човек може (и трябва) да постига целите си със собствените си ръце, със собствения си труд. Ако се запитаме: има ли проява на незачитане към някакъв "Бог" или "богове", то и в този случай ще трябва да отговорим с "Да": "Богът" и/или "боговете" са игнорирани по най-недвусмислен начин, след като дори и молитвата към "Него" и/или "тях" е отхвърлена като каквато и да било необходимост. При добро желание, във всяка подобна поговорка може да се съзре проява на високо самомнение, което е равностойно на богохулство, доколкото се отхвърля ролята на "Бога" или "боговете" в определено конкретно човешко дело, а оттам – и в човешките дела изобщо. Това представлява фактическо "говорене на 'големи думи' с гняв ('караница') към 'Бог'", независимо че дори думата "Бог" (в единствено или множествено число) не е спомената.

Обобщавайки (и заедно с това отчитайки евентуалните резултати, до които бихме достигнали, ако се потопим във всевъзможните теологични дълбини), бихме могли да заключим (отново!), че всяко изговаряне на "големи думи" би означавало някаква проява на "големеене" пред "Бога" или "боговете", на някакво самопоставяне на едно и също ниво с "Него" или "тях", поради което – дори и да се огласяват едни или други дреболии – те придобиват характера на "големи думи". А това – без каквото и да било съмнение – би следвало да е само по себе си вече крамолно. Ерго, трябва да се забрани не само "караницата с Бога", но и всяка "голяма дума". Вероятно, далеч не случайно, точно в такъв контекст, е влязла в употреба поговорката:

Както се вижда, и от тези допълнителни разсъждения се оказва, че в логическо отношение предложената за разглеждане поговорка:

е несъстоятелна.

1. В превода на "Метафизика" от Аристотел, публикуван през 2000 година от издателство "СОНМ", може да бъде прочетен следният текст:

“Всички започват от озадачаването – дали нещата са наистина така, както изглеждат: (...) когато става дума за [само]движещи се предмети или за слънцестоенията, или пък за несъизмеримостта на диаметъра. Тези неща изглеждат удивителни за всички, които все още не са установили причината за тях – удивително е да кажем, че има нещо, което не се измерва с най-малката мерна единица. (...) И наистина, нищо не би учудило един геометър повече от това, диаметърът да се окаже съизмерим” [с. 8].

2. Преводачът и редакторът на този фундаментален труд на Аристотел са намерили за необходимо да поместят бележка, свързана със спомената "несъизмеримост на диаметъра", която гласи следното:

“Може би става дума за несъизмеримост на диаметъра с окръжността. Това е факт, известен от многобройните питагорейски опити: при съотнасянето на числата, изразяващи дължината на окръжността и дължината на диаметъра, се получава константа, която не е цяло естествено число, а – както казваме ние днес – безкрайна непериодична дроб. (...) По времето на елинизма Архимед ще въведе съотношението 22 : 7, или дробта 22/7, по-късно наречена ‘числото пи’” [с. 307].

Фигура 1
Фигура 2

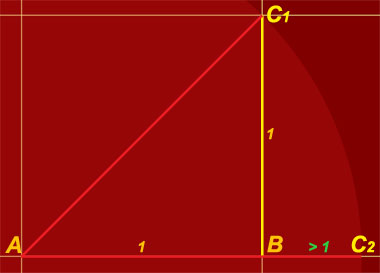
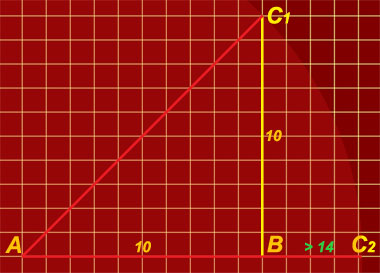
Пояснение. Въпросът относно съизмеримостта и/или несъизмеримостта на отсечки (и изобщо на части от едни или други линии, в това число и криви линии) е бил разглеждан през вековете като едно от най-сериозните предизвикателства пред човешката мисъл. В този сайт той е засегнат попътно в една публикация от 22-ри август 2008 година, включена в серията материали под названието "Опит за училище" ►►► . В поместената там интерпретация са използвани доказателствени средства, които могат да предизвикат някои затруднения. Ето защо тук е предложено кратко графично пояснение по въпроса.

ПИТА СЕ:

Прав ли е Аристотел, когато твърди, че диаметърът на една окръжност е несъизмерим спрямо нейната дължина? Прави ли са преводачът и редакторът на неговата "Метафизика", когато твърдят, че въпросните елементи на окръжността са в състояние на несъизмеримост, след като числата, които изразяват техните дължини се отнасят едно към друго под формата на константа, която "не е цяло естествено число", а "безкрайна непериодична дроб".

РЕШЕНИЕ:

Най-напред следва отново (и внимателно!) да се прочетат някои елементи от условието на задачата.

Първо. Нека бъде забелязано, че в цитирания текст от Аристотел се говори за "несъизмеримост на диаметъра" на една окръжност.

Второ. Нека бъде припомнен смисълът на понятието "съизмеримост" (респективно, "несъизмеримост"):

Тук не става дума за въвеждане на нови, необявени, части от условието на задачата, доколкото изискванията за съизмеримост-несъизмеримост са представени в цитирания коментар на преводача и редактора на Аристотеловата "Метафизика": положение на несъизмеримост се открива тогава, когато количественото съотношение между два съпоставяни геометрични обекта

Трето. Нека накрая бъде обърнато внимание върху последното изречение от въпросния коментар, с което се предлага историческа справка за откритието около съотношението между диаметъра на една окръжност и нейната обиколка. Казано е дословно:

В такъв случай, след като фактически обект на размисъл е съотношението между числителя и знаменателя на една дроб, представени чрез целите естествени числа 22 и 7, възниква въпросът: Какви са основанията да се твърди, че е налице някаква несъизмеримост? Налагащият се по необходимост отговор би следвало да бъде еднозначен: Никакви!

Тогава, какво да мислим за Аристотел?

Тук вече се появява нов проблем. Той е свързан с превода. Ако се погледне идентичният фрагмент от руската версия на "Метафизика", ще се забележи, че той гласи:

Независимо от степента на владеене на руски език, лесно може да се забележи, че на мястото на израза "несъизмеримост на диаметъра" тук стои друга словесна конфигурация: "несъизмеримост на диагонала". Но... между диаметър и диагонал има сериозна разлика!

Ако се погледне английският превод на същото място от "Метафизика" (например, в авторитетния сайт "Класически архив в интернет"), ще се открие следното:

И тук не е необходимо да се владее английски език, за да открие, че в превода се говори за "несъизмеримост на диагонала" вместо за Аристотеловата "несъизмеримост на диаметъра"!

Какво да се мисли в такъв случай? Защо едни преводачи говорят за диаметър на окръжност, а други – за диагонал на квадрат?

В такава обстановка е най-естествено да се потърси оригиналът. А той изглежда така, както е показано на копието вляво. (Тук за пореден път следва да се каже, че не е от голямо значение владеенето или невладеенето на старогръцки език. Достатъчно е да бъде забелязано, че Аристотел изрично говори за диаметър, а не за диагонал.)

И така, сблъскали сме се с изопачена при превода мисъл на автора? Или с негова техническа грешка, поправена от някои преводачи, но некоригирана (или незабелязана) от други?

Това е много сериозен въпрос. Някакви следващи размисли върху него могат да отидат далеч извън дефинираната задача и нейното решение. Така или иначе, видимо, Аристотел е приписал на съотношението между диаметъра на една окръжност и нейната обиколка качеството несъизмеримост, което не отговаря на действителното положение на нещата. Ако аз реша да построя две отсечки, едната от които да бъде дълга 22 сантиметра, а другата – 7 сантиметра, то те ще бъдат напълно съизмерими, доколкото общата мярка, с която ще могат да бъдат изразявани техните дължини, ще е сантиметърът. Абсолютно същото положение следва да бъде валидно и за обиколката на окръжността и нейния диаметър.

8. Въже около Земята

Фигура 1
Фигура 2

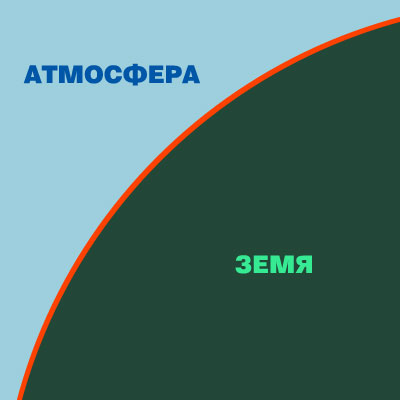
ДАДЕНО:

Нека бъде допуснато, че червената линия върху графиката отляво (фигура 1) представлява стилизирано въже, което е опасало плътно цялата Земя. Нека в случая Земята се разглежда като идеална сфера с диаметър 12 745 591 метра. Нека в добавка бъде прието, че въжето е изработено от материя, която не се разтегля и не се свива, а съединяването на двата му края един с друг (за да се получи цялостна обиколка около Земята) е изпълнено без какъвто и да било възел – с допирането на краищата му един до друг се е образувал необходимия обхващащ земното кълбо идеален обръч, разположен около идеалния земен диаметър.

Нека сега бъде допуснато, че някой е пожелал дължината на описаното въже да бъде увеличена така, че между него и сферичната повърхност на Земята да се получи тънък просвет, равен на 1 милиметър (фигура 2).

ПИТА СЕ:

От какъв порядък трябва да бъде увеличението в дължината на въжето, за да се постигне търсения просвет: няколко метра, няколко километра? Какво подсказва интуицията като предполагаем отговор?

РЕШЕНИЕ:

Отговорът на първия от поставените въпроси е: увеличението в дължината на въжето е от порядъка на милиметри. Доказателството е следното:

1. Диаметърът на окръжността, оформена от вътрешната страна на въжето, когато то е прилепено плътно до сферичната повърхност на идеалната Земя (фигура 1), възлиза на: 12 745 591 000 милиметра. Нека за удобство този диаметър да бъде обозначен като D1.

2. За да бъдат изпълнени началните условия на задачата, дължината на въжето трябва да е: 40 057 571 714,29 милиметра. Нека тази дължина бъде обозначена като S1 (S1 = D1 . π).

3. Диаметърът на окръжността, оформена от вътрешната страна на въжето (фигура 2), когато то трябва да опасва земната сфера с просвет от 1 милиметър над нея (D2), следва да е 12 745 591 002 милиметра: D2 = D1 + 2 (вследствие увеличението на диаметъра с по 1 милиметър във всяка една от неговите две посоки).

4. В този случай, дължината на въжето трябва да е вече: 40 057 571 720,57 милиметра. Нека тя бъде обозначена като S2 (S2 = D2 . π).

5. Разликата между S2 и S1 е: 6,28 милиметра (а ако се прецизира системата от закръгления – 6,29 милиметра).

Къде е парадоксалното в такъв случай?

То се съдържа в много от опитите да се отговори на втория поставен въпрос: "какво подсказва интуицията" в ситуация като настоящата?

От многото диалози, които съм имал по този повод с различни хора през годините мога да споделя, че техните отговори обикновено гравитират около "хиляди метри" или "стотици километри". Вероятно в случая нещо от човешките представи внушава, че щом някакво въже трябва да увеличи своята дължина така, че да стане възможна появата на просвет от 1 милиметър, но... около огромно сферично тяло, чиито размери се изразяват в десетки хиляди километри, то ще са необходими поне няколкостотин метра добавка към дължината на въпросното въже.

Дори и след надлежни изчисления такива хора гледат с нескрито подозрение към настоящата получена добавка от "6 и малко отгоре милиметра", за които – със сигурност – картинно си представят, че в своята нищожност те просто ще се "загубят" сред останалите десетки милиарди милиметри.

Подобно положение на нещата би следвало да култивира у всекиго един дежурен санитарен минимум скепсис по адрес на човешката интуиция (надлежно поставяна на най-висок пиедестал от трубадурите на някои учения).

ДОПЪЛНИТЕЛЕН КОМЕНТАР №1:

Скоро след обявяването на горното решение, на пощата на "Нова Магнаура" пристигна писмо със следния текст:

ДОПЪЛНИТЕЛЕН КОМЕНТАР №2:

През 1928 година известният математик Макс Ден произнася във Франкфуртския университет тържествена академична реч, озаглавена "Духовното своеобразие на математùка". Тя започва така:

Вероятно, за "средния" математик тази задача е безинтересна, защото знае нейното решение. (Впрочем, лично аз я чух преди много години от "висш" математик, който ми я представи именно в нейната "земна" конкретика, при което допусна грешка, огласявайки като отговор резултат от 1 милиметър.) В настоящия случай си мислех, че нейното съдържание може да бъде доловено по-лесно от всеки лаик, ако бъде представено с понятия, по-близки до обкръжаващия ни свят.

Илия Кожухаров

В "Евангелие от Лука" (7:28) съществува текст, в който се казва дословно (тук и надолу – правописът запазен):

“На другия ден Иисус отиваше в града, наречен Наùн; и с Него вървяха мнозина от учениците Му и много народ.

А когато се приближи до градските врата, ето, изнасяха мъртвец, едничък син на майка си, а тя беше вдовица; и много народ вървеше с нея от града.

Като я видя Господ, смили се над нея и рече ù: не плачи.

И като се приближи, допря се до носилото; носачите се спряха, и Той рече: Момко, тебе думам, стани!

Мъртвецът, като се подигна, седна и почна да говори; и Иисус го предаде на майка му.

И страх обвзе всички, и славеха Бога и казваха: велик пророк се издигна между нас, и Бог посети Своя народ.

Това мнение за Него се разнесе по цяла Иудея и по цялата околност.

И известиха на Иоана неговите ученици за всичко това.

Иоан, като повика двама свои ученици, изпрати ги при Иисуса да попитат: Ти ли си Оня, Който има да дойде, или другиго да чакаме?

А те, като дойдоха при Него, рекоха: Иоан Кръстител ни прати при Тебе да попитаме: Ти ли си Оня, Който има да дойде, или другиго да чакаме?

А в тоя час Той излекува мнозина от болести и недъзи и от зли духове и на мнозина слепи дарува зрение.

И отговори им Иисус и рече: идете и разкажете Иоану, каквото видяхте и чухте: слепи прогледват, хроми прохождат, прокажени се очистват, глухи прочуват, мъртви възкръсват, на бедни се благовествува (...).

След като заминаха изпратените от Иоана, Той почна да говори към народа за Иоана: какво излязохте в пустинята да видите? Тръстика ли, люлеена от вятъра?

Но какво излязохте да видите? Човек ли, облечен в меки дрехи? Ето, ония, които се обличат богато и живеят разкошно, са в царските палати.

Но какво тогава излязохте да видите? Пророк ли? Да, казвам ви, и повече от пророк.

Този е, за когото е писано: ‘Ето, Аз изпращам пред лицето Ти Моя Ангел, който ще приготви Твоя път пред Тебе.’

ПИТА СЕ:

Съществува ли противоречие в заключителното изречение?

РЕШЕНИЕ:

За да се установи наличието или отсъствието на каквото и да било противоречие, би следвало да се изследва педантично съдържанието на всяка дума и израз, изграждащи едно твърдение, както и смисловите връзки между тях. В текстове като този обаче – тук иде реч за текста, от който е направено предстоящото за коментар извлечение – присъства един фундаментален (и практически непреодолим) проблем. Той може да бъде обозначен по следния полушеговит – но всъщност, напълно реално отразяващ действителното положение на нещата – начин:

Гарван гарвану око може и да не вади, но парадокс парадокса вади! На бял свят! Постоянно!

Подобно съпътстващо обстоятелство може да предопредели не просто някакво пространно разгънато решение на поставения въпрос, но дори и такъв опит за доказателство, който е белязан с практическата невъзможност то да бъде доведено докрай. Когато една стъпка по изясняване на някакво смислово съдържание води мрежовидно до осъществяването на няколко следващи идентични стъпки, които на свой ред водят до лавинообразно идващи нови и нови подобни стъпки, угрозата от появата на потенциално препятствие пред желанието за поставяне на окончателна точка по въпроса се увеличава неимоверно.

Така или иначе, изглежда в случая е наложително да бъдат поставени на изясняване следните думи и фрази:

● "родените от жени",

● "пророк",

● "царството Божие", и

● "по-голям", респективно – "по-малък".

Едно важно предварително условие, което трябва непременно да бъде отбелязано, се отнася до необходимостта от съобразяване с факта, че твърдението, което ще се анализира, е разположено в цялостно изречение, имащо характера на обобщение. Поради тази причина, напълно естествено е да се приеме, че смисълът, който се влага в която и да било включена в него дума, се разпростира без варирания от началото до края на въпросното твърдение. В противен случай, би трябвало да има едни или други уточняващи разграничения. Това поне го изисква коректното боравене със словата.

И още, следващите надолу разсъждения могат да се сторят някому прекалено разточителни и обстоятелствени. В същото време, всяко тяхно лаконично представяне (така, както много хора обичат да постъпват) би се оказало незащитимо срещу много реални или мислими упреци.

Първо.

В случая изразът "родените от жени" трябва да обхваща: 1. всички хора, които фактически са били родени от жени, и 2. всички хора, за които в едни или други документи и текстове (в това число, и в легендарни религиозни текстове) се твърди, че са били родени от жени. Втората част от това предложено тълкувание се налага поради факта, че подложеното на изследване изречение е част от легендарен текст.

В съответствие с направеното уточнение, евангелските персонажи Иоан Кръстител и И(и)сус Христос се явяват членове на въпросното множество (на "родените от жени"), доколкото това се "доказва", примерно, със следния текст:

В следните редове се открива важно междинно съдържание:

В двете "зачевания" има известни различия. Около това при Елисавета се откроява известна неяснота във връзка с ролята на нейния съпруг. Ако обаче се допусне, че Захария – независимо от неговата "напреднала възраст" – си е възвърнал (по "Божията воля") оплодителната си способност, то той би могъл да се счита баща на бъдещия Йоан ("Предтеча" или "Кръстител"). Въпреки всичко има неяснота около намесата на "Светия Дух", който "изпълва" Елисавета едва в шестия месец от нейната бременност. Глаголът изпълва би могъл да се третира като своеобразно "божествено оплождане", доколкото – ако това не би се случило – Йоан би се оказал само един от многото обикновени мъже по земята. (А достатъчно ясно е, че по същия начин "Светият Дух" се е "спуснал" и над Мариам, което "предопределя" и особения статус на нейната бъдеща рожба.) При тези обстоятелства изглежда напълно естествено да се мисли, че участието на все същия "Свети Дух" следва да е обезсилило във висока степен (ако не и изцяло) биологичното бащинство на Захария, възвисявайки и бъдещия младенец Йоан до фактическото положение на "Божи син", а с това – и до полу-брат на И(и)сус по "бащина" линия.

Така или иначе, според евангелската легенда, двете "раждания от жени" се случват:

Второ.

Тук следва да се предложат някои пояснения около понятието "пророк".

Общият свод от текстове на Стария и Новия завет буквално гъмжи от пророци и от техните предсказания. Самата дума "пророк" се среща 339 пъти, нейното множествено число, "пророци" – 243 пъти, глаголът "пророкува" ("~м", "~ш", "~т") – 94 пъти, "пророчествува" ("~м", "~ш", "~т", "~ме", "~те") – 64 пъти, съществителното "пророчество(то)" – 67 пъти, неговото множествено число "пророчества(та)" – 14 пъти, "пророчица(та) – 9 пъти и така нататък.

Колкото и някой да приеме следващото уточнение за излишно, трябва да се посочи, че в новозаветните текстове и двете евангелски действащи лица се третират като имащи статут на пророци. Наистина, евангелист Йоан създава известни проблеми с един фрагмент от своето евангелие, в което описва как представители на юдеите – по-високопоставени и по-малко високопоставени свещеници – са изпратени да установят що за човек е Кръстителят:

Това обаче може да бъде изтълкувано като чисто литературен похват, имащ за цел да направи по-релефен онзи щрих от рисувания портрет, който засилва представата за едно съработничество в делото на И(и)сус, белязано с похвана скромност. Освен това, нека бъде отново прочетено вече споменатото свидетелство на самия И(и)сус, в което се казва:

А иначе, и Йоан, и И(и)сус се занимават с пророкуване. Едно от техните общи предсказания (и може би – най-важното!) е това за скорошното идване на "царството небесно".

Йоан Кръстител:

Тук вече следва да бъде поставен въпросът за коефициента на полезно действие около огласяваните предсказания. Както всеки подобен коефициент, и той би трябвало да се формира като дроб, в числителя на която стоят бройката сбъднали се пророчества, а в знаменателя – всички заявени. Не е изключено някаква подобна изследователска работа вече да е била извършена тук или там по света. По отношение на конкретно визираното пророчество обаче този коефициент се оказва практически нулев. Това превръща двамата пророци във фактически лъжепророци.

Ето основанията.

Строго погледнато, в непосредствено цитираните по-горе изречения не се съдържа конкретно предсказание. Има само съобщение за това, че "царството небесно" се е приближило. В същото време обаче е огласено настойчиво увещание за покаяние. То е формулирано така, че да предизвика сериозна тревога: ако покаянието не бъде извършено скоро и навреме, то непокаялият се ще бъде застигнат от въпросното "царство" в своето греховно състояние и ще получи надлежно наказание. Това означава, че онези, към които е отправено предупреждението, трябва да почувстват не просто и не само близкото местонахождение на все същото "царство", но и опасността във всеки момент то да се стовари с всичката си страховитост върху непокаялия се. В противен случай, простото съобщение, че някъде наблизо се намира нещо, което (чисто теоретично, но без каквато и да било практическа осъществимост) може да създаде някому някакви главоболия – такова съобщение би послужило единствено като повод за насмешки по адрес на неговия глашатай. Следователно, коментираните призиви следва да се третират като носещи в себе си смисъла на предсказания.

В добавка, тези призиви трябва да бъдат мислени като съотносими, примерно, с продължителността на един човешки живот. Защото: какъв смисъл би могла да има една или друга заплаха от идването на "царството небесно", ако това би се случило след нечия смърт – обстоятелство, при което никакво покаяние не би могло да бъде сторено? При тези обстоятелства, призивът за каене следва да се третира като предупреждение, което иска да внуши, че се очаква "събитие", предстоящо в рамките на някакви близки години, ако не и месеци или седмици. Все това въздействие трябва да оказват определени реплики, приписвани на И(и)сус и повтаряни от неговите следовници.

Например:

Или:

(Тук "времето се изпълни" е само един употребяван в евангелската лексика силно емоционално въздействащ израз-заместител за "скоро, много скоро".)

Или:

(Попътно. Морално ли е един "Бог", който има власт над целия Всемир, който може да превръща земни люде в "богове", да "забавя" своята защита към избраниците си? За справка – Библия, "Втора книга Мойсеева (Изход)", 7:1: "Но Господ рече на Моисея: виж, Аз те поставих за Бог фараону; а брат ти Аарон ще бъде твой пророк...". И също попътно. Морално ли е един "Бог" да има "избраници"?)

Нататък:

Или (заканителна реплика на И(и)сус):

Или:

Или – финални думи, "верни и истински":

И аз, Иоан, гледах и чувах това. А когато чух и видях, паднах да се поклоня пред нозете на Ангела, който ми казваше това;

а той ми казваше: стой, не прави това! понеже аз съм съслужител твой и на братята ти пророци и на ония, които пазят думите на тая книга; Богу се поклони.

Неправедният нека върши още неправда; нечистият нека се още скверни; праведният нека върши още правда, а светият нека се още осветява.

Аз съм Алфа и Омега, начало и край, Първият и Последният.

Блажени са, които изпълняват заповедите Му, за да имат право да ядат от дървото на живота и да влязат в града през портите.

А отвън са псетата, магьосниците, блудниците, убийците, идолослужителите и всеки, който обича и върши лъжа.

Аз, Иисус, изпратих Своя Ангел да ви засвидетелствува това в църквите. Аз съм коренът и родът Давидов, утрената и светла звезда.

И Духът и невестата казват: дойди! и който чува, да каже: дойди! и който е жаден, да дойде, и който желае, нека взема от водата на живота даром.

И аз свидетелствувам всекиму, който слуша пророчествените думи на тая книга: ако някой прибави нещо към тях, нему Бог ще наложи поразите, за които е писано в тая книга;

и ако някой отнеме нещо от думите на книгата на това пророчество, Бог ще отнеме дела му от книгата на живота и от светия град и от написаното в тая книга.

Благодатта на Господа нашего Иисуса Христа да бъде с всички вас. Амин” [пак там, 22:1-21].

С тези редове на дълбока екзалтация завършва така нареченото "Свето Писание" на християните. Всеки, който ги прочете, би трябвало да се изпълни с трепетно очакване за едно най-близко предстоящо идване на "царството небесно". На какъвто и език да е била изговорена или написана думата "скоро" или фразата "времето е близко", смисълът не би следвало да се измерва с хиляди години, защото в такъв случай моралната оценка на подобен акт би била проста и неподлежаща на съмнение: лъжа!

И тук не могат да помогнат уговорки от рода на следната:

доколкото "върховната разпоредителна сила" е имала предостатъчно време да "открие човека на греха", въпросния "син на погибелта", и да го срази за вечни времена.

Не е лесно да се приеме, че за така закъснялата повторна среща с все същата "върховна сила" сме виновни самите ние, доколкото не сме предприели някои подсказани ни между редовете необходими стъпки:

Не е възможно да решим, че "царството Божие" междувременно е дошло – в съответствие със съдържанието на следната мисъл, приписана на Христос:

И поради друго куриозно твърдение не е никак лесно да се приеме, че така очакваното "царство" е дошло :

Нали, според един от по-пестеливо обрисуваните сценарии на това събитие, "скорото дохождане на Божия ден" ще се съпътства от "пламнали небеса", които ще се разрушат, и от "разгорели се стихии", които ще се стопят, за да можем ние, в съответствие с "обещанието" на И(и)сус да дочакаме

Разбираемо, отчетено към днешна дата, коментираното предсказание не се е сбъднало. Нито някакво "ново небе" се е появило, нито се е появила някаква "нова земя", на които "обитава правда". Следователно, никакво "царство Божие" не е дошло. Нещо повече, не се забелязва то и да се е "приближило" или да се е настанило "вътре в нас". В такъв случай, въпросните евангелски персонажи – поне в своята пророческа функция на вестители за идването на "съдния ден" (това трябва да бъде изречено повторно) – са се провалили.

Такова заключение обаче би могло да бъде обявено за невярно, поради типично светския модел на разсъждение, приложен при неговото извеждане. В добавка, би могло да се посочи, че е засвидетелствано и едно основно неразбиране на иносказателния библейски и – особено – евангелски език, често декориран с обилие от използвани притчи. Такива обструкции съставляват стандартния богословски упрек, нещо като предварително готов универсален словесен отпор срещу всяка светска критика. Освен това, тук може да бъде добавено и не по-малко стандартното обвинение в ползване на фрагменти от текстове, извадени от техния контекст. Това налага известен коментар.

Що се отнася до съотношението между текст и контекст, обилието от цитирани дотук фрагменти от новозаветните книги (нещо, което може и да е предизвикало досада у мнозина) би трябвало да е свело до разумния минимум всяко притеснение за евентуално волно или неволно изкривяване на вложения идеен смисъл. А припомнянето на цялата последна глава от "Откровение на Йоан Богослов" идва да удовлетвори и всяко искане за контекстуално позоваване. Както би могло да се забележи обаче, внушаваното във всички предложени фрагменти усещане е за пришествие, което е непосредствено предстоящо.

Относно иносказателния език и обилно използвания стил на говорене "с притчи", следва да се обърне внимание върху факта, че това съвсем не може да бъде достойнство на който и да било подобен текст. Когато се излага учение, което има за цел да бъде основополагащо за една целокупна регулация на обществения живот, всяко мъгляво говорене се превръща в неизчерпаем източник за неразбирателства, борби, амбициозни опити за налагане на едни тълкувания над други, схизми, разцепления – с други думи, то води до резултат, диаметрално противоположен на онзи, който е бивал предпоставян. Поради тази причина – независимо от дежурното отношение на религиозно преклонение – подобен стил не може да има каквото и да било оправдание, независимо че той се оказва заложен като откровено признато намерение:

Ако един учител излага по такъв начин своето педагогическо верую, той е достоен единствено за порицание. А този "учител" попътно е и "Бог", надарен с всичкото могъщество, за което и сам претендира. Тогава подобни думи са само жалко признание за безсилие.

В добавка, самата идея да се смесват иносказателни с неиносказателни мисли е повече от вредоносна, защото напълно естествено нейното прилагане би довело до всеобща невъзможност да се прекара неоспорима граница между едните и другите. Ето пример. В своята страст по алегорично говорене И(и)сус споделя с учениците си:

Човек може да види в представите си как един актьор изиграва този фрагмент, показвайки с набор от ярки театрални или филмови средства удовлетворението на оратора от откритата и предложена алегория. Но... един от най-големите християнски писатели на късната античност, Ориген (около 185 – около 254), посветил се още от юношеска възраст на най-педантично изучаване на юдейските и християнски текстове, самият той превърнал се в един от най-ревностните пропагандатори на новото учение, изследовател, посветил се на изключително задълбочено критично сравняване и изучаване на противоречията между различните езикови версии на едни и същи религиозни писания, съчинил стотици религиозни беседи, адресирани към възможно най-широк кръг слушатели и поради това издържани в дух на достъпност, създал многочислени коментари на "свещени текстове", в които отделял два смисъла: един буквален (и поради това – нисш) и друг духовен (съответно – висш)... та, същият този Ориген сам кастрирал себе си в резултат на буквалното възприемане на горните стихове от евангелист Матей. Вероятно, той е сторил това в състояние на върховен екстаз, упоен от мисълта, че по такъв начин би отнел всяка възможност за упрек относно евентуално влизане в непозволени учителски контакти със своите възпитаници: мъже и жени. И вероятно към това е прибавил и самовнушението, че така се е извисил до неописуемо съвършенство.

Всякакъв род подобни примери обаче би трябвало да се запишат по сметката на въпросното мъгляво иносказателно говорене и писане. И попътно да убедят всеки, който се прехласва по такъв тип словесност, в нейното вредоносно въздействие, когато тя се оказва непомерно експонирана и неразумно възвеличавана.

Трето.

Относно израза "царство Божие", следва да се посочи (нещо, което вероятно е станало ясно от примерите дотук), че той се използва като практически синонимен с изрази като: "царство небесно", "Твоето царство" или "царството на Христа и Бога", или "царството на Господа нашего и Неговия Христос" – в каквото, междувременно, следва да се превърне "царството на света" (всичко това, както за царството на "Бога Отец", така и на "Бога Син"), "царството на Бога", "царството на Отца", "царството Му (Си)" или "Своето царство", или "Своето небесно царство", или "Моето царство", или "царството Ми", или "вечното царство на Господа нашего и Спасителя Иисуса Христа", или "царството на възлюбления Си Син", или "Царството Иисус Христово", или "царството на нашия Бог" (за царството на "Сина Человечески").

Цялата посочена синонимия се обединява от идеята за "Евангелието на царството" – сиреч, от "Благата вест за царството", което е едно и само едно.

Четвърто.

Изразите "по-голям" и "по-малък", смислово отнесени към пророческите способности на Йоан Кръстител и И(и)сус Христос създават сериозни тълкувателни проблеми. Освен това, на фона на все още несбъдналото се тяхно централно предсказание, всеки опит за претегляне на каквато и да било тяхна "пророческа сила" не изглежда много смислено занимание. Все пак, някакво усилие в това направление би могло да бъде направено, единствено в ареала на легендарните текстове.

Не е невъзможно едно първо тълкувание да бъде насочено към възрастта на двете действащи лица. Според писанията – и ако двете раждания са се осъществили след нормално продължила бременност – Йоан Кръстител би трябвало да е по-възрастен от И(и)сус Христос с шест месеца. В този смисъл, обичайно е някой, който е "батко", да бъде определян като "по-голям". (Естествено, след подобно припомняне се налага да се направи уговорката, че това далеч не може да бъде сигурно за народи, които са живели преди хилядолетия и които биха могли да са следвали напълно различни езикови традиции.)

От друга страна обаче, контекстът, в който се намира тук поставеното за анализ твърдение, е свързан с питането: що за човек е Йоан Кръстител? Пророк ли е? А не: на колко години е:

фактически се признава, че Йоан Кръстител е владелецът на най-висшите пророчески способности сред одухотворените същества. Естествено, от този списък трябва да бъде изваден, да речем, Богът-Отец, доколкото за него няма никакви писмени свидетелства, че е "роден от жена", както и персонажите Адам и Ева, тъй като те също не са "родени от жена".

Допълнително, идеята за възрастова ориентация на въпросните сравнителни определения трябва да се отхвърли като несъстоятелна и въз основа на една интригуваща реплика на самия Йоан Кръстител, който казва по адрес на И(и)сус:

Както лесно може да се съобрази, не е възможно "смаляването" да се отнася до биологичната възраст. Не би следвало да е възможно и нещо друго обаче: "Богът И(и)сус" да не знае за тази мисъл на Йоан Кръстител, защото в противен случай той не би следвало да бъде никакъв бог. (Дефинитивно, боговете трябва да знаят всичко, което е било, е и ще бъде.) В такъв случай, ако изреченото от Йоан Кръстител за "растежа" и "смаляването" е било прието от И(и)сус като напълно естествено, то втората част от подложеното на анализ изречение:

би трябвало да изглежда по малко по-различен начини:

или:

Точно такъв текст обаче отсъства. Ерго, противоречието е налице.

А то, вградено в едни "божествени" думи, вместо да подреди и без това не много стройните мисли на човеците, само би ги объркало още повече.

В добавка би следвало да се отхвърли евентуалната обструкция, по силата на която единият от персонажите трябва да се мисли като пребиваващ в "царството Божие", а другият (Йоан Кръстител) – в "царството на Дявола", Земята. Изразът "по-малкият в царството Божие" фактически закрепва и "по-малкия" и "по-големия" към едни и същи селения, независимо дали тяхната (на И(и)сус и на Йоан) "големина" се мисли преди или след засвидетелствания логически парадокс.

Естествено, тук някой може да обърне внимание върху факта, че на фона на големите идеи, които се лансират от християнството, един парадокс от рода на констатирания би следвало да се разглежда като нещо незначително. Но... ако бъдат припомнени следващите думи на Христос, адресирани към неговите ученици:

то може с основание да се попита:

Подобни примери изпълват надлъж и нашир "Писанието" – това писание, което много хора по света са приели като лична пътеводна светлина, с всяка негова дума. Те не забелязват никаква парадоксалност. Те дори не допускат наличието на каквато и да било парадоксалност. Така са научени.

Подобни хора ще възразят срещу изложените дотук разсъждения и направения извод. Нещо повече, голяма част от тях няма да стигнат до тези последни редове, защото още от самото им начало, ще установят, че тук се говорят неща, които могат да се окажат вредни за вярата им. Някои, все пак, биха изтъкнали едни или други контрааргументи. Един такъв контрааргумент би насочил вниманието към онези евентуалните текстови неточности, които са могли да се получат при превода на античните текстове на съвременни езици.

Но... такъв аргумент следва веднага да насочи мисълта към факта, че във всеки идентичен случай – какъвто и превод да се е ползвал или ползва тук и там днес – с него са били форматирани мислите на милиони хора. Тогава, напълно закономерно може да се попита: не е ли било естествено локалните наместници на "Бога" да са били водени от такова "божествено" прозрение, изпратено им от "Светия Дух", което да ги предпази от каквито и да било грешки при представянето на самото "Божие слово"? А и самият "Бог" – ако е забелязал, че нейде се пишат и четат някакви изопачени "Негови" мисли – не е ли било редно да изпрати ясен знак, с който да поправи допусканите грешки? Например, да изгори с огън, който не би причинил пожар, онези Библии из човешките домове, които не предават точно думите "Му". Или да изличи грешните слова и на тяхно място, сторвайки чудо, да изпише правилния превод.

За "Него" това не би трябвало да бъде невъзможно.

ДАДЕНО:

По-долу са показани резултатите, получени при използването на два метода в хирургичното лечение на камъни в бъбреците. При първия метод ("А") се прави голям отвор, за да се достигне до бъбреците и да се извадят образуваните в тях камъни, докато при втория ("В") операцията се осъществява през малък отвор.

И при двата метода случаите на хирургическа намеса са разделени на: интервенции, при които са изваждани малки камъни, и интервенции, при които са изваждани големи камъни. Данните показват следната надеждност:

Изглежда напълно естествено да се направи заключението: първият метод на лечение е по-надежден, доколкото и при двата вида хирургични интервенции процентът на успешните лечения е по-голям (93,10% срещу 86,67% и 73,00% срещу 68,75%).

ПИТА СЕ:

Правомерен ли е предложеният извод?

РЕШЕНИЕ:

Налагащият се като очевиден извод, посочен в "Дадено", изглежда неподлежащ на каквото и да било съмнение: Първият метод е по-надежден! В същото време, достатъчно е да се извърши едно сумиране на всички данни за всеки от двата метода, за да се открие изненадващ резултат:

Тук вече изводът – и в абсолютното изражение на броя успешно излекувани пациенти, и в проценти – би гласял: Вторият метод е по-надежден!

Защо се получава така? – това е един неминуемо пораждащ се въпрос. Как е възможно обобщението на двойки количествени данни, при които една група резултати показва недвусмислено превъзходство над друга идентична група, в крайна сметка да обръща общия извод в диаметрално противоположна посока? Нещо повече, ако от нашия извод биха зависели последващи решения от жизненоважно естество, ние – видимо – бихме допуснали ужасяваща грешка, избирайки метод "А" като "по-успешен" (и изоставяйки метод "В" като "по-неуспешен")! Впрочем, едно обръщане към историята (не непременно българската, а и общочовешката) вероятно би ни дало множество примери в потвърждение на това наше мимолетно появило се прозрение.

В търсене на отговор за причините, поради които се проявява коментираната парадоксална ситуация, бихме могли да забележим, че общият брой пациенти с диагноза "малки бъбречни камъни", лекувани по метод "А", са чувствително по-малко, отколкото пациентите със същата диагноза, лекувани по метод "В". И обратно, пациентите с диагноза "големи бъбречни камъни", лекувани по метод "А", са чувствително повече, отколкото пациентите със същата диагноза, лекувани по метод "В". След подобно разкритие можем да бъдем споходени от идеята, че нещо в теглата на значимост, с които участват различните групи пациенти, лекувани по единия и другия метод, играе важна (но оставаща някак скрита!) роля в изчислителните процедури.

В подобна ситуация можем да проведем един мислен експеримент. Нека се опитаме да намалим разликите в броя пациенти, диагностицирани с двата вида диагнози и лекувани по двата метода, но така, че регистрираната успеваемост да се запази във възможно най-близки до първоначалните стойности. Например, нека увеличим числото на диагностицираните с "малки бъбречни камъни" (и лекувани по метод "А") от 87 на 97, като в същото време намалим числото на диагностицираните с "големи бъбречни камъни" от 263 на 253. Нека заедно с това коригираме и бройката на успешно излекуваните пациенти (по метод "А") така, че данните за успеваемост на терапията да се запазят максимално близки до първоначалните. Нека извършим същите промени и с числата, имащи отношение към прилагането на метод "В". В такъв случай бихме получили следния резултат:

Веднага се забелязва, че при приблизително еднакви предимства в успеваемостта на метод "А" спрямо метод "В" (разгледана по видове диагнози) и при запазено предимство на метод "В" спрямо метод "А" (като обобщени данни – вж. табличните клетки, оцветени в тъмносиво), въпросното предимство е намаляло; от 82,57% към 78,00% се е намалило до 82,00% към 78,57%.

Този резултат може да ни подтикне към следваща подобна стъпка. Нека тя бъде по-смела, нека по-малките числа на лекувани пациенти бъдат увеличени по-чувствително и нека със същата бройка да бъдат намалени по-големите числа пациенти. С цел да се запазят приблизително процентите на успеваемост, нека съответно бъдат коригирани и числата, сочещи успешно излекуваните пациенти. Една примерна версия на данните би могла да изглежда така:

Както се вижда, при приблизително запазване на началните стойности за терапевтична успеваемост при двата метода и двата вида диагнози, сумарната преценка, получена върху чувствително завишен брой пациенти с "малки бъбречни камъни", съчетани с идентично занижаване на броя пациенти с "големи бъбречни камъни" (всички те, лекувани по метода "А"), както и при съответните обратни промени при другата група пациенти (лекувани по метода "В"), общата картина показва практически изравнена успеваемост.

На това място е важно да се подчертае следният факт: нищо в двата метода, "А" и "В", не е претърпяло промяна. Доколкото става въпрос за мисловни вариации върху конкретен базисен експеримент, пациентите са дефинитивно лекувани по един и същ начин, при това – и при запазена процентна ефективност на избраното лечение. Единствените промени, които са правени във вариациите върху все същия базисен експеримент, се отнасят само до бройката, а оттам – и до (някак невидимото) тегло на значимост на отделните резултати в общия сборен ефект от приложението на двата метода.

Накрая, бихме могли да си представим такава мислена експериментална стъпка, при която табличните данни изглеждат по следния начин:

Тук процентите за конкретната успеваемост на лечението при пациентите с двата вида диагнози, лекувани по двата метода са абсолютно еднакви с първоначалните: 93,10% срещу 86,67%; 73,00% срещу 68,75%. Единствено бройката подложени на лечение лица е променена: във всяка от четирите групи тя е от по 10 000 души. Изводът е повече от красноречив: Първият метод е по-надежден!

Какво можем да мислим при такъв пореден резултат? В крайна сметка: метод "А" или метод "В" е по-надежден? И какъв отговор да бъде даден след разсъжденията, през които сме преминали и които са оставили у нас усещането, че основанията на мислите ни наподобяват подвижни пясъци: онова, което в даден момент ни изглежда сигурно и убедително, в следващата минута рухва безостатъчно, за да се въздигне отново след време като истина?!

Изглежда разумно да си помогнем по следния начин: трябва да съобразим извода си с данните от втората таблица по-горе. Сиреч, трябва да заключим, че метод "В" е по-надежден! И наистина, всички следващи разсъждения представляват само предположения, основаващи се на мисловни проекции, породени от някакъв кръг реални опитни данни. Строго погледнато, зад никоя от следващите таблици не стои никакъв фактически проведен експеримент. Ние само предположихме, че различната успешност при отделните методи на лечение – такава, каквато е показана в първата и втората таблица – би могла да се ползва като някаква константна величина. Но... това – нека бъде повторено! – е само наше предположение.

Ако искаме да останем при фактите, трябва да отсъдим, че МЕТОД "В" Е ПО-УСПЕШЕН. Всяко друго решение би било само бягство от фактите. И подслоняване върху някакви непотвърдени прогнози.

Впрочем, така описаният парадокс е известен на човечеството (не цялото, разбира се!) едва от ХХ век. И може само да се гадае за планините от случаи, при които хората са вземали погрешни решения, попадайки в капаните на собствените си идеализации по отношение на игрите с числа.

12. В издателството

ПРЕДВАРИТЕЛНА БЕЛЕЖКА:

Предходният пример на статистически парадокс предизвика оживени реакции. Напълно възможно е у някого да е останало частично съмнение в коректността на предложените доказателствени разсъждения. По тази причина надолу е поместен още един пример, третиращ идентична ситуация. Тя изглежда по-опростена в сравнение с предходната.

ДАДЕНО:

В едно издателство работят двама редактори: X и Y. Ангажиментите им се свеждат до задължението да прочитат и коригират одобрени за печат научни статии. В края на една от работните седмици се оказва, че редактор Х не е успял да приключи с нито една от трите предоставени му статии, а редактор Y се е справил само с един от седемте възложени му текста. В края на следващата седмица рекапитулацията е: редактор Х е редактирал пет от седемте предоставени му статии, а редактор Y – всичките три разпределени към него текста. Таблично, успеваемостта на двамата редактори може да бъде представена така:

Изглежда напълно естествено да се направи заключението: в своята работа редактор Y показва по-висока резултатност от редактор Х, доколкото и през двете седмици броят (и процентът) на редактираните от него статии е по-голям (14,29% срещу 0,00% и 100,00% срещу 71,43%).

ПИТА СЕ:

Правомерен ли е предложеният извод?

РЕШЕНИЕ:

Както и при предходната задача, добре е отговорът да бъде потърсен след едно обединение на резултатите от работата на редакторите през двете седмици.

Веднага се забелязва, че – при еднакъв брой възложени текстове – заключението следва да е: в своята работа редактор Х е показал по-висока резултатност от редактор Y (50,00% срещу 40,00%).

13. БНТ: прогноза за безработицата през 2016 година

ДАДЕНО:

Във вечерната информационна емисия на Българската национална телевизия "По света и у нас" на 12-ти май 2014 година бе съобщено дословно:

За по-голяма убедителност съобщението бе придружено от графична илюстрация:

ПИТА СЕ:

Какъв ще бъде процентът на безработните в България, ако прогнозата на БАН се сбъдне?

РЕШЕНИЕ:

Условието на задачата смущава. В същото време – както всеки може да се убеди след справка в сайта на БНТ – то възпроизвежда дословно текста и графиката, които бяха огласени и показани в рубриката "По света и у нас" от 12-ти май 2014 година.

Как би могъл да разсъждава редовият зрител/слушател?

Никак не е изключено той да постъпи така, както би постъпил в много други подобни случаи. Например, ако чуе по Българското национално радио, че нивото на река Дунав при града Х е спаднало с 20 сантиметра и понастоящем е 490 сантиметра, той ще съобрази, че в предходния ден е било 510 сантиметра, доколкото 510 – 20 = 490 сантиметра.

В случая с безработицата той ще долови някаква липса на данни за нивото на безработицата от времето преди да е започнал периодът на нейното прогнозно спадане. Разбира се, такъв зрител/слушател може да потърси липсващата му информация, при което – обръщайки се към сайта на Националния статистически институт – би открил следното:

Следвайки своя мисловен стереотип (и предполагайки, че междувременно, към началото на май 2014 година безработицата в България е все същата като тази от края на 2013 година), той ще понечи да извади от официално регистрираното нейно ниво (12,9%) съобщеното предполагаемо намаление (20%) и в резултат ще получи удивителното отрицателно число: – 7,1%. Оттук веднага би трябвало да последва изводът, че към 2016 година в България няма да има нито един безработен гражданин на възраст "15 и повече навършени години", поради което – за да решим националните си трудово-борсови проблеми – ще се наложи да внасяме работници и служители от чужбина.

Дори и тези пресмятания (както и следващият ги извод) да не бъдат направени, съобщението за намаление на безработицата с 20% е толкова внушително, че можем да си представим как световните осведомителни агенции са го разнесли мигновено по света, който на минутата е започнал да гледа на Отечеството ни като най-привлекателната за труд точка на планетата.

Практическата невъзможност на лансираната перспектива може би ще бъде забелязана от някакъв малък процент зрители/слушатели, които ще разтълмят енигматичното послание на БНТ така: 20% трябва да се пресметнат като дробна част от последно констатираното фактическо ниво на безработицата, при което резултатът би изглеждал чувствително по-различно:

0,2 х 0,129 = 0,0258,

или 2,58%

Нека обаче бъде сравнено съобщението за 20% с някакво съобщение за 2,58%.

Каква неприятна разлика между двете разлики!

14. "Можеш да бягаш..."

ДАДЕНО: